Rectangular waveguides are th one of the earliest type of the transmission lines. They are used in many applications. A lot of components such as isolators, detectors, attenuators, couplers and slotted lines are available for various standard waveguide bands between 1 GHz to above 220 GHz.
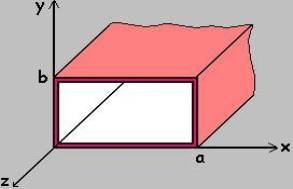
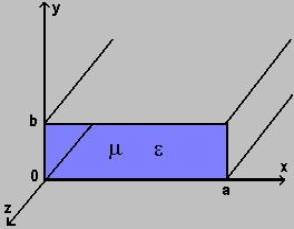
A rectangular waveguide supports TM and TE modes but not TEM waves because we cannot define a unique voltage since there is only one conductor in a rectangular waveguide. The shape of a rectangular waveguide is as shown below. A material with permittivity e and permeability m fills the inside of the conductor.
A rectangular waveguide cannot propagate below some certain frequency. This frequency is called the cut-off frequency.
Here, we will discuss TM mode rectangular waveguides and TE mode rectangular waveguides separately. Lets start with the TM mode´
- TM Modes
Consider the shape of the rectangular waveguide above with dimensions a and b (assume a>b) and the parameters e and m. For TM waves Hz = 0 and Ez should be solved from equation for TM mode;
Ñ2xy Ez0 + h2 Ez0 = 0
Since Ez(x,y,z) = Ez0(x,y)e-gz, we get the following equation,
If we use the method of separation of variables, that is Ez0(x,y)=X(x).Y(y) we get,
Since the right side contains x terms only and the left side contains y terms only, they are both equal to a constant. Calling that constant as kx2, we get;
where ky2=h2-kx2
Now, we should solve for X and Y from the preceding equations. Also we have the boundary conditions of;
Ez0(0,y)=0
Ez0(a,y)=0
Ez0(x,0)=0
Ez0(x,b)=0
From all these, we conclude that
X(x) is in the form of sin kxx, where kx=mp/a, m=1,2,3,
Y(y) is in the form of sin kyy, where ky=np/b, n=1,2,3,
So the solution for Ez0(x,y) is
From ky2=h2-kx2, we have;
From these equations, we get
where
Here, m and n represent possible modes and it is designated as the TMmn mode. m denotes the number of half cycle variations of the fields in the x-direction and n denotes the number of half cycle variations of the fields in the y-direction.
When we observe the above equations we see that for TM modes in rectangular waveguides, neither m nor n can be zero. This is because of the fact that the field expressions are identically zero if either m or n is zero. Therefore, the lowest mode for rectangular waveguide TM mode is TM11 .
Here, the cut-off wave number is
At a given operating frequency f, only those frequencies, which have fc<="" modes="" not="" or="" p="" propagate.="" such="" that="" the="" to="" which="" will="" with="">
The mode with the lowest cut-off frequency is called the dominant mode. Since TM modes for rectangular waveguides start from TM11 mode.
- TE Mode
Consider again the rectangular waveguide below with dimensions a and b (assume a>b) and the parameters e and m.
For TE waves Ez = 0 and Hz should be solved from equation for TE mode;
Ñ2xy Hz + h2 Hz = 0
Since Hz(x,y,z) = Hz0(x,y)e-gz, we get the following equation,
If we use the method of separation of variables, that is Hz0(x,y)=X(x).Y(y) we get,
Since the right side contains x terms only and the left side contains y terms only, they are both equal to a constant. Calling that constant as kx2, we get
Publicado por: Jahir Alonzo Linares Mora
C.I: 19769430 CRF









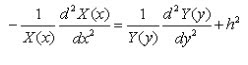

No hay comentarios:
Publicar un comentario